[40 Pa.B. 5903]
[Saturday, October 16, 2010]

[Continued from previous Web Page]

MATHEMATICS—HIGH SCHOOL—MODELING

 Modeling links classroom mathematics and statistics to everyday life, work, and decision-making. Modeling is the process of choosing and using appropriate mathematics and statistics to analyze empirical situations, to understand them better, and to improve decisions. Quantities and their relationships in physical, economic, public policy, social, and everyday situations can be modeled using mathematical and statistical methods. When making mathematical models, technology is valuable for varying assumptions, exploring consequences, and comparing predictions with data.

 A model can be very simple, such as writing total cost as a product of unit price and number bought, or using a geometric shape to describe a physical object like a coin. Even such simple models involve making choices. It is up to us whether to model a coin as a three-dimensional cylinder, or whether a two-dimensional disk works well enough for our purposes. Other situations—modeling a delivery route, a production schedule, or a comparison of loan amortizations—need more elaborate models that use other tools from the mathematical sciences. Real-world situations are not organized and labeled for analysis; formulating tractable models, representing such models, and analyzing them is appropriately a creative process. Like every such process, this depends on acquired expertise as well as creativity.

 Some examples of such situations might include:

 • Estimating how much water and food is needed for emergency relief in a devastated city of 3 million people, and how it might be distributed.

 • Planning a table tennis tournament for 7 players at a club with 4 tables, where each player plays against each other player.

 • Designing the layout of the stalls in a school fair so as to raise as much money as possible.

 • Analyzing stopping distance for a car.

 • Modeling savings account balance, bacterial colony growth, or investment growth.

 • Engaging in critical path analysis, e.g., applied to turnaround of an aircraft at an airport.

 • Analyzing risk in situations such as extreme sports, pandemics, and terrorism.

 • Relating population statistics to individual predictions.

 In situations like these, the models devised depend on a number of factors: How precise an answer do we want or need? What aspects of the situation do we most need to understand, control, or optimize? What resources of time and tools do we have? The range of models that we can create and analyze is also constrained by the limitations of our mathematical, statistical, and technical skills, and our ability to recognize significant variables and relationships among them. Diagrams of various kinds, spreadsheets and other technology, and algebra are powerful tools for understanding and solving problems drawn from different types of real-world situations.

 

 

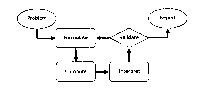
 One of the insights provided by mathematical modeling is that essentially the same mathematical or statistical structure can sometimes model seemingly different situations. Models can also shed light on the mathematical structures themselves, for example, as when a model of bacterial growth makes more vivid the explosive growth of the exponential function.

 The basic modeling cycle is summarized in the diagram. It involves (1) identifying variables in the situation and selecting those that represent essential features, (2) formulating a model by creating and selecting geometric, graphical, tabular, algebraic, or statistical representations that describe relationships between the variables, (3) analyzing and performing operations on these relationships to draw conclusions, (4) interpreting the results of the mathematics in terms of the original situation, (5) validating the conclusions by comparing them with the situation, and then either improving the model or, if it is acceptable, (6) reporting on the conclusions and the reasoning behind them. Choices, assumptions, and approximations are present throughout this cycle.

 In descriptive modeling, a model simply describes the phenomena or summarizes them in a compact form. Graphs of observations are a familiar descriptive model—for example, graphs of global temperature and atmospheric CO₂ over time.

 Analytic modeling seeks to explain data on the basis of deeper theoretical ideas, albeit with parameters that are empirically based; for example, exponential growth of bacterial colonies (until cut-off mechanisms such as pollution or starvation intervene) follows from a constant reproduction rate. Functions are an important tool for analyzing such problems.

 Graphing utilities, spreadsheets, computer algebra systems, and dynamic geometry software are powerful tools that can be used to model purely mathematical phenomena (e.g., the behavior of polynomials) as well as physical phenomena.

 Modeling Standards Modeling is best interpreted not as a collection of isolated topics but rather in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (*).

MATHEMATICS—HIGH SCHOOL—GEOMETRY

 An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts—interpreting a schematic drawing, estimating the amount of wood needed to frame a sloping roof, rendering computer graphics, or designing a sewing pattern for the most efficient use of material.

 Although there are many types of geometry, school mathematics is devoted primarily to plane Euclidean geometry, studied both synthetically (without coordinates) and analytically (with coordinates). Euclidean geometry is characterized most importantly by the Parallel Postulate, that through a point not on a given line there is exactly one parallel line. (Spherical geometry, in contrast, has no parallel lines.)

 During high school, students begin to formalize their geometry experiences from elementary and middle school, using more precise definitions and developing careful proofs. Later in college some students develop Euclidean and other geometries carefully from a small set of axioms.

 The concepts of congruence, similarity, and symmetry can be understood from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combinations of these, all of which are here assumed to preserve distance and angles (and therefore shapes generally). Reflections and rotations each explain a particular type of symmetry, and the symmetries of an object offer insight into its attributes—as when the reflective symmetry of an isosceles triangle assures that its base angles are congruent.

 In the approach taken here, two geometric figures are defined to be congruent if there is a sequence of rigid motions that carries one onto the other. This is the principle of superposition. For triangles, congruence means the equality of all corresponding pairs of sides and all corresponding pairs of angles. During the middle grades, through experiences drawing triangles from given conditions, students notice ways to specify enough measures in a triangle to ensure that all triangles drawn with those measures are congruent. Once these triangle congruence criteria (ASA, SAS, and SSS) are established using rigid motions, they can be used to prove theorems about triangles, quadrilaterals, and other geometric figures.

 Similarity transformations (rigid motions followed by dilations) define similarity in the same way that rigid motions define congruence, thereby formalizing the similarity ideas of ''same shape'' and ''scale factor'' developed in the middle grades. These transformations lead to the criterion for triangle similarity that two pairs of corresponding angles are congruent.

 The definitions of sine, cosine, and tangent for acute angles are founded on right triangles and similarity, and, with the Pythagorean Theorem, are fundamental in many real-world and theoretical situations. The Pythagorean Theorem is generalized to non-right triangles by the Law of Cosines. Together, the Laws of Sines and Cosines embody the triangle congruence criteria for the cases where three pieces of information suffice to completely solve a triangle. Furthermore, these laws yield two possible solutions in the ambiguous case, illustrating that Side-Side-Angle is not a congruence criterion.

 Analytic geometry connects algebra and geometry, resulting in powerful methods of analysis and problem solving. Just as the number line associates numbers with locations in one dimension, a pair of perpendicular axes associates pairs of numbers with locations in two dimensions. This correspondence between numerical coordinates and geometric points allows methods from algebra to be applied to geometry and vice versa. The solution set of an equation becomes a geometric curve, making visualization a tool for doing and understanding algebra. Geometric shapes can be described by equations, making algebraic manipulation into a tool for geometric understanding, modeling, and proof. Geometric transformations of the graphs of equations correspond to algebraic changes in their equations.

 Dynamic geometry environments provide students with experimental and modeling tools that allow them to investigate geometric phenomena in much the same way as computer algebra systems allow them to experiment with algebraic phenomena.

 Connections to Equations. The correspondence between numerical coordinates and geometric points allows methods from algebra to be applied to geometry and vice versa. The solution set of an equation becomes a geometric curve, making visualization a tool for doing and understanding algebra. Geometric shapes can be described by equations, making algebraic manipulation into a tool for geometric understanding, modeling, and proof.

Geometry Overview

Congruence	• Experiment with transformations in the plane. • Understand congruence in terms of rigid motions. • Prove geometric theorems. • Make geometric constructions.	1. Apply geometric concepts in modeling situations 2. Mathematical Practices 3. Make sense of problems and persevere in solving them. 4. Reason abstractly and quantitatively.	Mathematical Practices
Similarity, Right Triangles, and Trigonometry	• Understand similarity in terms of similarity transformations. • Prove theorems involving similarity. • Define trigonometric ratios and solve problems involving right triangles. • Apply trigonometry to general triangles.	5. Construct viable arguments and critique the reasoning of others. 6. Model with mathematics. 7. Use appropriate tools strategically. 8. Attend to precision. 9. Look for and make use of structure. 10. Look for and express regularity in repeated reasoning.
Circles         Expressing Geometric Properties with Equations       Geometric Measurement and Dimension       Modeling with Geometry	• Understand and apply theorems about circles. • Find arc lengths and areas of sectors of circles.   • Translate between the geometric description and the equation for a conic section. • Use coordinates to prove simple geometric theorems algebraically.   • Explain volume formulas and use them to solve problems. • Visualize relationships between two-dimensional and three-dimensional objects.   • Apply geometric concepts in modeling situations.

Congruence _G-CO

Experiment with transformations in the plane.

 1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc.

 2. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).

 3. Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself.

 4. Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.

 5. Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify

a sequence of transformations that will carry a given figure onto another.

Understand congruence in terms of rigid motions.

 6. Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.

 7. Use the definition of congruence in terms of rigid motions to show that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent.

 8. Explain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from the definition of congruence in terms of rigid motions.

Prove geometric theorems.

 9. Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment's endpoints.

 10. Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point.

 11. Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals of a parallelogram bisect each other, and conversely, rectangles are parallelograms with congruent diagonals.

Make geometric constructions.

 12. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.

 13. Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle.

Similarity, Right Triangles, and Trigonometry _G-SRT

Understand similarity in terms of similarity transformations.

 1. Verify experimentally the properties of dilations given by a center and a scale factor:

 a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged.

 b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor.

 2. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.

 3. Use the properties of similarity transformations to establish the AA criterion for two triangles to be similar.

Prove theorems involving similarity.

 4. Prove theorems about triangles. Theorems include: a line parallel to one side of a triangle divides the other two proportionally, and conversely; the Pythagorean Theorem proved using triangle similarity.

 5. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures.

Define trigonometric ratios and solve problems involving right triangles.

 6. Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.

 7. Explain and use the relationship between the sine and cosine of complementary angles.

 8. Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.*

Apply trigonometry to general triangles.

 9. (+) Derive the formula A = 1/2 ab sin(C) for the area of a triangle by drawing an auxiliary line from a vertex perpendicular to the opposite side.

 10. (+) Prove the Laws of Sines and Cosines and use them to solve problems.

 11. (+) Understand and apply the Law of Sines and the Law of Cosines to find unknown measurements in right and non-right triangles (e.g., surveying problems, resultant forces).

Circles _G-C

Understand and apply theorems about circles.

 1. Prove that all circles are similar.

 2. Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.

 3. Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle.

 4. (+) Construct a tangent line from a point outside a given circle to the circle.

Find arc lengths and areas of sectors of circles.

 5. Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

Expressing Geometric Properties with Equations _G-GPE

Translate between the geometric description and the equation for a conic section.

 1. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.

 2. Derive the equation of a parabola given a focus and directrix.

 3. (+) Derive the equations of ellipses and hyperbolas given the foci, using the fact that the sum or difference of distances from the foci is constant.

Use coordinates to prove simple geometric theorems algebraically.

 4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, RADICAL3) lies on the circle centered at the origin and containing the point (0, 2).

 5. Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point).

 6. Find the point on a directed line segment between two given points that partitions the segment in a given ratio.

 7. Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.*

Geometric Measurement and Dimension _G-GMD

Explain volume formulas and use them to solve problems.

 1. Give an informal argument for the formulas for the circumference of a circle, area of a circle, volume of a cylinder, pyramid, and cone. Use dissection arguments, Cavalieri's principle, and informal limit arguments.

 2. (+) Give an informal argument using Cavalieri's principle for the formulas for the volume of a sphere and other solid figures.

 3. Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.*

Visualize relationships between two-dimensional and three-dimensional objects.

 4. Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.

Modeling with Geometry _G-MG

Apply geometric concepts in modeling situations.

 1. Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).*

 2. Apply concepts of density based on area and volume in modeling situations (e.g., persons per square mile, BTUs per cubic foot).*

 3. Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints or minimize cost; working with typographic grid systems based on ratios).*

MATHEMATICS—HIGH SCHOOL—STATISTICS AND PROBABILITY*

 Decisions or predictions are often based on data—numbers in context. These decisions or predictions would be easy if the data always sent a clear message, but the message is often obscured by variability. Statistics provides tools for describing variability in data and for making informed decisions that take it into account.

 Data are gathered, displayed, summarized, examined, and interpreted to discover patterns and deviations from patterns. Quantitative data can be described in terms of key characteristics: measures of shape, center, and spread. The shape of a data distribution might be described as symmetric, skewed, flat, or bell shaped, and it might be summarized by a statistic measuring center (such as mean or median) and a statistic measuring spread (such as standard deviation or interquartile range). Different distributions can be compared numerically using these statistics or compared visually using plots. Knowledge of center and spread are not enough to describe a distribution. Which statistics to compare, which plots to use, and what the results of a comparison might mean, depend on the question to be investigated and the real-life actions to be taken.

 Randomization has two important uses in drawing statistical conclusions. First, collecting data from a random sample of a population makes it possible to draw valid conclusions about the whole population, taking variability into account. Second, randomly assigning individuals to different treatments allows a fair comparison of the effectiveness of those treatments. A statistically significant outcome is one that is unlikely to be due to chance alone, and this can be evaluated only under the condition of randomness. The conditions under which data are collected are important in drawing conclusions from the data; in critically reviewing uses of statistics in public media and other reports, it is important to consider the study design, how the data were gathered, and the analyses employed as well as the data summaries and the conclusions drawn.

 Random processes can be described mathematically by using a probability model: a list or description of the possible outcomes (the sample space), each of which is assigned a probability. In situations such as flipping a coin, rolling a number cube, or drawing a card, it might be reasonable to assume various outcomes are equally likely. In a probability model, sample points represent outcomes and combine to make up events; probabilities of events can be computed by applying the Addition and Multiplication Rules. Interpreting these probabilities relies on an understanding of independence and conditional probability, which can be approached through the analysis of two-way tables.

 Technology plays an important role in statistics and probability by making it possible to generate plots, regression functions, and correlation coefficients, and to simulate many possible outcomes in a short amount of time.

 Connections to Functions and Modeling. Functions may be used to describe data; if the data suggest a linear relationship, the relationship can be modeled with a regression line, and its strength and direction can be expressed through a correlation coefficient.

Statistics and Probability Overview

Interpreting Categorical and Quantitative Data             Making Inferences and Justifying Conclusions           Conditional Probability and the Rules of Probability           Using Probability to Make Decisions

• Summarize, represent, and interpret data on a single count or measurement variable. • Summarize, represent, and interpret data on two categorical and quantitative variables. • Interpret linear models.   • Understand and evaluate random processes underlying statistical experiments. • Make inferences and justify conclusions from sample surveys, experiments and observational studies.   • Understand independence and conditional probability and use them to interpret data. • Use the rules of probability to compute probabilities of compound events in a uniform probability model.   • Calculate expected values and use them to solve problems. • Use probability to evaluate outcomes of decisions.

1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning.

Mathematical Practices

Interpreting Categorical and Quantitative Data _S-ID

Summarize, represent, and interpret data on a single count or measurement variable.

 1. Represent data with plots on the real number line (dot plots, histograms, and box plots).

 2. Use statistics appropriate to the shape of the data distribution to compare center (median, mean) and spread (interquartile range, standard deviation) of two or more different data sets.

 3. Interpret differences in shape, center, and spread in the context of the data sets, accounting for possible effects of extreme data points (outliers).

 4. Use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets, and tables to estimate areas under the normal curve.

Summarize, represent, and interpret data on two categorical and quantitative variables.

 5. Summarize categorical data for two categories in two-way frequency tables. Interpret relative frequencies in the context of the data (including joint, marginal, and conditional relative frequencies). Recognize possible associations and trends in the data.

 6. Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.

 a. Fit a function to the data; use functions fitted to data to solve problems in the context of the data. Use given functions or choose a function suggested by the context. Emphasize linear, quadratic, and exponential models.

 b. Informally assess the fit of a function by plotting and analyzing residuals.

 c. Fit a linear function for a scatter plot that suggests a linear association.

Interpret linear models.

 7. Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.

 8. Compute (using technology) and interpret the correlation coefficient of a linear fit.

 9. Distinguish between correlation and causation.

Making Inferences and Justifying Conclusions _S-IC

Understand and evaluate random processes underlying statistical experiments.

 1. Understand statistics as a process for making inferences to be made about population parameters based on a random sample from that population.

 2. Decide if a specified model is consistent with results from a given data-generating process, e.g., using simulation. For example, a model says a spinning coin falls heads up with probability 0.5. Would a result of 5 tails in a row cause you to question the model?

Make inferences and justify conclusions from sample surveys, experiments, and observational studies.

 3. Recognize the purposes of and differences among sample surveys, experiments, and observational studies; explain how randomization relates to each.

 4. Use data from a sample survey to estimate a population mean or proportion; develop a margin of error through the use of simulation models for random sampling.

 5. Use data from a randomized experiment to compare two treatments; use simulations to decide if differences between parameters are significant.

 6. Evaluate reports based on data.

Conditional Probability and the Rules of Probability _S-CP

Understand independence and conditional probability and use them to interpret data.

 1. Describe events as subsets of a sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions, intersections, or complements of other events (''or,'' ''and,'' ''not'').

 2. Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent.

 3. Understand the conditional probability of A given B as P(A and B)/P(B), and interpret independence of A and B as saying that the conditional probability of A given B is the same as the probability of A, and the conditional probability of B given A is the same as the probability of B.

 4. Construct and interpret two-way frequency tables of data when two categories are associated with each object being classified. Use the two-way table as a sample space to decide if events are independent and to approximate conditional probabilities. For example, collect data from a random sample of students in your school on their favorite subject among math, science, and English. Estimate the probability that a randomly selected student from your school will favor science given that the student is in tenth grade. Do the same for other subjects and compare the results.

 5. Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer.

Use the rules of probability to compute probabilities of compound events in a uniform probability model.

 6. Find the conditional probability of A given B as the fraction of B's outcomes that also belong to A, and interpret the answer in terms of the model.

 7. Apply the Addition Rule, P(A or B) = P(A) + P(B) - P(A and B), and interpret the answer in terms of the model.

 8. (+) Apply the general Multiplication Rule in a uniform probability model, P(A and B) = P(A)P(B|A) = P(B)P(A|B), and interpret the answer in terms of the model.

 9. (+) Use permutations and combinations to compute probabilities of compound events and solve problems.

Using Probability to Make Decisions _S-MD

Calculate expected values and use them to solve problems.

 1. (+) Define a random variable for a quantity of interest by assigning a numerical value to each event in a sample space; graph the corresponding probability distribution using the same graphical displays as for data distributions.

 2. (+) Calculate the expected value of a random variable; interpret it as the mean of the probability distribution.

 3. (+) Develop a probability distribution for a random variable defined for a sample space in which theoretical probabilities can be calculated; find the expected value. For example, find the theoretical probability distribution for the number of correct answers obtained by guessing on all five questions of a multiple-choice test where each question has four choices, and find the expected grade under various grading schemes.

 4. (+) Develop a probability distribution for a random variable defined for a sample space in which probabilities are assigned empirically; find the expected value. For example, find a current data distribution on the number of TV sets per household in the United States, and calculate the expected number of sets per household. How many TV sets would you expect to find in 100 randomly selected households?

Use probability to evaluate outcomes of decisions.

 5. (+) Weigh the possible outcomes of a decision by assigning probabilities to payoff values and finding expected values.

 a. Find the expected payoff for a game of chance. For example, find the expected winnings from a state lottery ticket or a game at a fast-food restaurant.

 b. Evaluate and compare strategies on the basis of expected values. For example, compare a high-deductible versus a low-deductible automobile insurance policy using various, but reasonable, chances of having a minor or a major accident.

 6. (+) Use probabilities to make fair decisions (e.g., drawing by lots, using a random number generator).

 7. (+) Analyze decisions and strategies using probability concepts (e.g., product testing, medical testing, pulling a hockey goalie at the end of a game).

NOTE ON COURSES AND TRANSITIONS

 The high school portion of the Standards for Mathematical Content specifies the mathematics all students should study for college and career readiness. These standards do not mandate the sequence of high school courses. However, the organization of high school courses is a critical component to implementation of the standards. To that end, sample high school pathways for mathematics—in both a traditional course sequence (Algebra I, Geometry, and Algebra II) as well as an integrated course sequence (Mathematics 1, Mathematics 2, Mathematics 3)—will be made available shortly after the release of the final Common Core State Standards. It is expected that additional model pathways based on these standards will become available as well.

 The standards themselves do not dictate curriculum, pedagogy, or delivery of content. In particular, states may handle the transition to high school in different ways. For example, many students in the U.S. today take Algebra I in the 8th grade, and in some states this is a requirement. The K-7 standards contain the prerequisites to prepare students for Algebra I by 8th grade, and the standards are designed to permit states to continue existing policies concerning Algebra I in 8th grade.

 A second major transition is the transition from high school to post-secondary education for college and careers. The evidence concerning college and career readiness shows clearly that the knowledge, skills, and practices important for readiness include a great deal of mathematics prior to the boundary defined by (+) symbols in these standards. Indeed, some of the highest priority content for college and career readiness comes from Grades 6-8. This body of material includes powerfully useful proficiencies such as applying ratio reasoning in real-world and mathematical problems, computing fluently with positive and negative fractions and decimals, and solving real-world and mathematical problems involving angle measure, area, surface area, and volume. Because important standards for college and career readiness are distributed across grades and courses, systems for evaluating college and career readiness should reach as far back in the standards as Grades 6-8. It is important to note as well that cut scores or other information generated by assessment systems for college and career readiness should be developed in collaboration with representatives from higher education and workforce development programs, and should be validated by subsequent performance of students in college and the workforce.

GLOSSARY

 Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction of two whole numbers with whole number answers, and with sum or minuend in the range 0-5, 0-10, 0-20, or 0-100, respectively. Example: 8 + 2 = 10 is an addition within 10, 14 - 5 = 9 is a subtraction within 20, and 55 - 18 = 37 is a subtraction within 100.

 Additive inverses. Two numbers whose sum is 0 are additive inverses of one another. Example: 3/4 and - 3/4 are additive inverses of one another because 3/4 + (- 3/4) = (- 3/4) + 3/4 = 0.

 Associative property of addition. See Table 3 in this Glossary.

 Associative property of multiplication. See Table 3 in this Glossary.

 Bivariate data. Pairs of linked numerical observations. Example: a list of heights and weights for each player on a football team.

 Box plot. A method of visually displaying a distribution of data values by using the median, quartiles, and extremes of the data set. A box shows the middle 50% of the data.²⁹

 Commutative property. See Table 3 in this Glossary.

 Complex fraction. A fraction A/B where A and/or B are fractions (B nonzero).

 Computation algorithm. A set of predefined steps applicable to a class of problems that gives the correct result in every case when the steps are carried out correctly. See also: computation strategy.

 Computation strategy. Purposeful manipulations that may be chosen for specific problems, may not have a fixed order, and may be aimed at converting one problem into another. See also: computation algorithm.

 Congruent. Two plane or solid figures are congruent if one can be obtained from the other by rigid motion (a sequence of rotations, reflections, and translations).

 Counting on. A strategy for finding the number of objects in a group without having to count every member of the group. For example, if a stack of books is known to have 8 books and 3 more books are added to the top, it is not necessary to count the stack all over again; one can find the total by counting on—pointing to the top book and saying ''eight,'' following this with ''nine, ten, eleven. There are eleven books now.''

 Dot plot. See: line plot.

 Dilation. A transformation that moves each point along the ray through the point emanating from a fixed center, and multiplies distances from the center by a common scale factor.

 Expanded form. A multidigit number is expressed in expanded form when it is written as a sum of single-digit multiples of powers of ten. For example, 643 = 600 + 40 + 3.

 Expected value. For a random variable, the weighted average of its possible values, with weights given by their respective probabilities.

 First quartile. For a data set with median M, the first quartile is the median of the data values less than M. Example: For the data set {1, 3, 6, 7, 10, 12, 14, 15, 22, 120}, the first quartile is 6.³⁰ See also: median, third quartile, interquartile range.

 Fraction. A number expressible in the form a/b where a is a whole number and b is a positive whole number. (The word fraction in these standards always refers to a nonnegative number.) See also: rational number.

 Identity property of 0. See Table 3 in this Glossary.

 Independently combined probability models. Two probability models are said to be combined independently if the probability of each ordered pair in the combined model equals the product of the original probabilities of the two individual outcomes in the ordered pair.

 Integer. A number expressible in the form a or -a for some whole number a.

 Interquartile Range. A measure of variation in a set of numerical data, the interquartile range is the distance between the first and third quartiles of the data set. Example: For the data set {1, 3, 6, 7, 10, 12, 14, 15, 22, 120}, the interquartile range is 15 - 6 = 9. See also: first quartile, third quartile.

 Line plot. A method of visually displaying a distribution of data values where each data value is shown as a dot or mark above a number line. Also known as a dot plot.³¹

 Mean. A measure of center in a set of numerical data, computed by adding the values in a list and then dividing by the number of values in the list.³² Example: For the data set {1, 3, 6, 7, 10, 12, 14, 15, 22, 120}, the mean is 21.

 Mean absolute deviation. A measure of variation in a set of numerical data, computed by adding the distances between each data value and the mean, then dividing by the number of data values. Example: For the data set {2, 3, 6, 7, 10, 12, 14, 15, 22, 120}, the mean absolute deviation is 20.

 Median. A measure of center in a set of numerical data. The median of a list of values is the value appearing at the center of a sorted version of the list—or the mean of the two central values, if the list contains an even number of values. Example: For the data set {2, 3, 6, 7, 10, 12, 14, 15, 22, 90}, the median is 11.

 Midline. In the graph of a trigonometric function, the horizontal line half-way between its maximum and minimum values.

 Multiplication and division within 100. Multiplication or division of two whole numbers with whole number answers, and with product or dividend in the range 0-100. Example: 72 ÷ 8 = 9.

 Multiplicative inverses. Two numbers whose product is 1 are multiplicative inverses of one another. Example: 3/4 and 4/3 are multiplicative inverses of one another because 3/4 × 4/3 = 4/3 × 3/4 = 1.

 Number line diagram. A diagram of the number line used to represent numbers and support reasoning about them. In a number line diagram for measurement quantities, the interval from 0 to 1 on the diagram represents the unit of measure for the quantity.

 Percent rate of change. A rate of change expressed as a percent. Example: if a population grows from 50 to 55 in a year, it grows by 5/50 = 10% per year.

 Probability distribution. The set of possible values of a random variable with a probability assigned to each.

 Properties of operations. See Table 3 in this Glossary.

 Properties of equality. See Table 4 in this Glossary.

 Properties of inequality. See Table 5 in this Glossary.

 Properties of operations. See Table 3 in this Glossary.

 Probability. A number between 0 and 1 used to quantify likelihood for processes that have uncertain outcomes (such as tossing a coin, selecting a person at random from a group of people, tossing a ball at a target, testing for a medical condition).

 Probability model. A probability model is used to assign probabilities to outcomes of a chance process by examining the nature of the process. The set of all outcomes is called the sample space, and their probabilities sum to 1. See also: uniform probability model.

 Random variable. An assignment of a numerical value to each outcome in a sample space.

 Rational expression. A quotient of two polynomials with a non-zero denominator. Rational number. A number expressible in the form a/b or - a/b for some fraction a/b. The rational numbers include the integers.

 Rectilinear figure. A polygon all angles of which are right angles.

 Rigid motion. A transformation of points in space consisting of a sequence of one or more translations, reflections, and/or rotations. Rigid motions are here assumed to preserve distances and angle measures.

 Repeating decimal. The decimal form of a rational number. See also: terminating decimal.

 Sample space. In a probability model for a random process, a list of the individual outcomes that are to be considered.

 Scatter plot. A graph in the coordinate plane representing a set of bivariate data. For example, the heights and weights of a group of people could be displayed on a scatter plot.³³

 Similarity transformation. A rigid motion followed by a dilation.

 Tape diagram. A drawing that looks like a segment of tape, used to illustrate number relationships. Also known as a strip diagram, bar model, fraction strip, or length model.

 Terminating decimal. A decimal is called terminating if its repeating digit is 0.

 Third quartile. For a data set with median M, the third quartile is the median of the data values greater than M. Example: For the data set {2, 3, 6, 7, 10, 12, 14, 15, 22, 120}, the third quartile is 15. See also: median, first quartile, interquartile range.

 Transitivity principle for indirect measurement. If the length of object A is greater than the length of object B, and the length of object B is greater than the length of object C, then the length of object A is greater than the length of object C. This principle applies to measurement of other quantities as well.

 Uniform probability model. A probability model which assigns equal probability to all outcomes. See also: probability model.

 Vector. A quantity with magnitude and direction in the plane or in space, defined by an ordered pair or triple of real numbers.

 Visual fraction model. A tape diagram, number line diagram, or area model.

 Whole numbers. The numbers 0, 1, 2, 3, . . . .

Table 1. Common addition and subtraction situations.³⁴

	Result Unknown	Change Unknown	Start Unknown
Add to	Two bunnies sat on the grass. Three more bunnies hopped there. How many bunnies are on the grass now? 2 + 3 = ?	Two bunnies were sitting on the grass. Some more bunnies hopped there. Then there were five bunnies. How many bunnies hopped over to the first two? 2 + ? = 5	Some bunnies were sitting on the grass. Three more bunnies hopped there. Then there were five bunnies. How many bunnies were on the grass before? ? + 3 = 5
Take from	Five apples were on the table. I ate two apples. How many apples are on the table now? 5 - 2 = ?	Five apples were on the table. I ate some apples. Then there were three apples. How many apples did I eat? 5 - ? = 3	Some apples were on the table. I ate two apples. Then there were three apples. How many apples were on the table before? ? - 2 = 3
	Total Unknown	Addend Unknown	Both Addends Unknown35
Put Together/ Take Apart36	Three red apples and two green apples are on the table. How many apples are on the table? 3 + 2 = ?	Five apples are on the table. Three are red and the rest are green. How many apples are green? 3 + ? = 5, 5 - 3 = ?	Grandma has five flowers. How many can she put in her red vase and how many in her blue vase? 5 = 0 + 5, 5 = 5 + 0 5 = 1 + 4, 5 = 4 + 1 5 = 2 + 3, 5 = 3 + 2
	Difference Unknown	Bigger Unknown	Smaller Unknown
Compare37	(''How many more?'' version): Lucy has two apples. Julie has five apples. How many more apples does Julie have than Lucy? (''How many fewer?'' version): Lucy has two apples. Julie has five apples. How many fewer apples does Lucy have than Julie? 2 + ? = 5, 5 - 2 = ?	(Version with ''more''): Julie has three more apples than Lucy. Lucy has two apples. How many apples does Julie have? (Version with ''fewer''): Lucy has 3 fewer apples than Julie. Lucy has two apples. How many apples does Julie have? 2 + 3 = ?, 3 + 2 = ?	(Version with ''more''): Julie has three more apples than Lucy. Julie has five apples. How many apples does Lucy have? (Version with ''fewer''): Lucy has 3 fewer apples than Julie. Julie has five apples. How many apples does Lucy have? 5 - 3 = ?, ? + 3 = 5

Table 2. Common multiplication and division situations.³⁸

	Unknown Product	Group Size Unknown (''How many in each group?'' Division)	Number of Groups Unknown (''How many groups?'' Division)
	3 × 6 = ?	3 × ? = 18 and 18 ÷ 3 = ?	? × 6 = 18 and 18 ÷ 6 = ?
Equal Groups	There are 3 bags with 6 plums in each bag. How many plums are there in all? Measurement example. You need 3 lengths of string, each 6 inches long. How much string will you need altogether?	If 18 plums are shared equally into 3 bags, then how many plums will be in each bag? Measurement example. You have 18 inches of string, which you will cut into 3 equal pieces. How long will each piece of string be?	If 18 plums are to be packed 6 to a bag, then how many bags are needed? Measurement example. You have 18 inches of string, which you will cut into pieces that are 6 inches long. How many pieces of string will you have?
Arrays,39 Area40	There are 3 rows of apples with 6 apples in each row. How many apples are there? Area example. What is the area of a 3 cm by 6 cm rectangle?	If 18 apples are arranged into 3 equal rows, how many apples will be in each row? Area example. A rectangle has area 18 square centimeters. If one side is 3 cm long, how long is a side next to it?	If 18 apples are arranged into equal rows of 6 apples, how many rows will there be? Area example. A rectangle has area 18 square centimeters. If one side is 6 cm long, how long is a side next to it?
Compare	A blue hat costs $6. A red hat costs 3 times as much as the blue hat. How much does the red hat cost? Measurement example. A rubber band is 6 cm long. How long will the rubber band be when it is stretched to be 3 times as long?	A red hat costs $18 and that is 3 times as much as a blue hat costs. How much does a blue hat cost? Measurement example. A rubber band is stretched to be 18 cm long and that is 3 times as long as it was at first. How long was the rubber band at first?	A red hat costs $18 and a blue hat costs $6. How many times as much does the red hat cost as the blue hat? Measurement example. A rubber band was 6 cm long at first. Now it is stretched to be 18 cm long. How many times as long is the rubber band now as it was at first?
General	a × b = ?	a × ? = p and p ÷ a = ?	? × b = p and p ÷ b = ?

Table 3. The properties of operations.

 Here a, b and c stand for arbitrary numbers in a given number system. The properties of operations apply to the rational number system, the real number system, and the complex number system.

Associative property of addition Commutative property of addition Additive identity property of 0 Existence of additive inverses   Associative property of multiplication Commutative property of multiplication Multiplicative identity property of 1 Existence of multiplicative inverses   Distributive property of multiplication over addition	(a + b) + c = a + (b + c) a + b = b + a a + 0 = 0 + a = a For every a there exists -a so that a + (-a) = (-a) + a = 0.   (a × b) × c = a × (b × c) a × b = b × a a × 1 = 1 × a = a For every a ≠ 0 there exists 1/a so that a × 1/a = 1/a × a = 1.   a × (b + c) = a × b + a × c

Table 4. The properties of equality.

 Here a, b and c stand for arbitrary numbers in the rational, real, or complex number systems.

Reflexive property of equality Symmetric property of equality Transitive property of equality Addition property of equality Subtraction property of equality Multiplication property of equality Division property of equality Substitution property of equality

a = a If a = b, then b = a. If a = b and b = c, then a = c. If a = b, then a + c = b + c. If a = b, then a - c = b - c. If a = b, then a × c = b × c. If a = b and c ≠ 0, then a ÷ c = b ÷ c. If a = b, then b may be substituted for a in any expression containing a.

Table 5. The properties of inequality.

 Here a, b and c stand for arbitrary numbers in the rational or real number systems.

Exactly one of the following is true: a < b, a = b, a > b. If a > b and b > c then a > c. If a > b, then b < a. If a > b, then -a < -b. If a > b, then a + c > b + c. If a > b and c > 0, then a × c > b × c. If a > b and c < 0, then a × c < b × c. If a > b and c > 0, then a × c > b × c. If a > b and c < 0, then a × c < b × c.

____

 ²⁹ Adapted from Wisconsin Department of Public Instruction, http://dpi.wi.gov/standards/mathglos.html, accessed March 2, 2010.

 ³⁰ Many different methods for computing quartiles are in use. The method defined here is sometimes called the Moore and McCabe method. See Langford, E., ''Quartiles in Elementary Statistics,'' Journal of Statistics Education Volume 14, Number 3 (2006),

 ³¹ Adapted from Wisconsin Department of Public Instruction, op. cit.

 ³² To be more precise, this defines the arithmetic mean.

 ³³ Adapted from Wisconsin Department of Public Instruction, op. cit.

 ³⁴ Adapted from Box 2-4 of Mathematics Learning in Early Childhood, National Research Council (2009, pp. 32, 33).

 ³⁵ These take apart situations can be used to show all the decompositions of a given number. The associated equations, which have the total on the left of the equal sign, help children understand that the = sign does not always mean makes or results in but always does mean is the same number as.

 ³⁶ Either addend can be unknown, so there are three variations of these problem situations. Both Addends Unknown is a productive extension of this basic situation especially for small numbers less than or equal to 10.

 ³⁷ For the Bigger Unknown or Smaller Unknown situations, one version directs the correct operation (the version using more for the bigger unknown and using less for the smaller unknown). The other versions are more difficult.

 ³⁸ The first examples in each cell are examples of discrete things. These are easier for students and should be given before the measurement examples.

 ³⁹ The language in the array examples shows the easiest form of array problems. A harder form is to use the terms rows and columns: The apples in the grocery window are in 3 rows and 6 columns. How many apples are in there? Both forms are valuable.

 ⁴⁰ Area involves arrays of squares that have been pushed together so that there are no gaps or overlaps, so array problems include these especially important measurement situations.

[Pa.B. Doc. No. 10-1962. Filed for public inspection October 15, 2010, 9:00 a.m.]

[40 Pa.B. 5999]
[Saturday, October 16, 2010]

 

---

No part of the information on this site may be reproduced for profit or sold for profit.

This material has been drawn directly from the official Pennsylvania Bulletin full text database. Due to the limitations of HTML or differences in display capabilities of different browsers, this version may differ slightly from the official printed version.

---